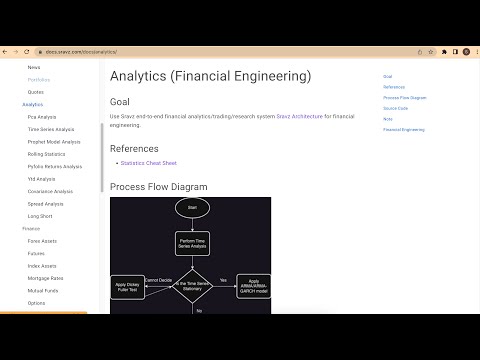
Time Series Analysis
Peforms time series analysis on assets and portfolios.
Timeseries Analysis - Screenshot
Code explanation video
Source Code
Use Case
- Verify if timeseries model can be used to predict stock price
- Verify if the timeseries is stationary or a random work (white noise)
Analysis
- AdjustedClose Price Vs Date
- Price is upwards trending overtime
- Price shows sesonality
- AdjustedClose Price first difference vs Date
- Plots
$$ p_t - p_{t-1} $$
Vs Date - Removes trend (Upwards/Downwards movement of price)
- Plot is centered around 0
- Variance is still present. Lot of fluctuation around 0
- Variance today is higher than the variance in the past (data is increasing expotentially)
- Plots
- ln(AdjustedClose Price) vs Date plot to convert exponential curve to linear curve
- AdjustedClose Price original variance (The divergence of data from its mean value) vs Date
- Plot 30 days moving variance with Date
$$ \sigma^2 = \frac{\displaystyle\sum_{i=1}^{n}(x_i - \mu)^2} {n} $$
- Minor variance in price does not show in the plot
- Plot 30 days moving variance with Date
- AdjustedClose Price log variance vs Date
- Plot 30 days log price moving variance with Date
- Log price moving average smooths the variance
- We see variance through out the time series
- Minor variance in enhanced and shows in the plot
- ln(Adjusted Close Price Variance) vs Date makes the variance relatively constant
- ln(AdjustedClose Price) first difference vs Date
- Enhances the variance through out the time series
- Better represenation of variance.
- Series is stationary (Differencing makes the timeseries stationary)
- Auto Correlation plot - AdjustedClose Price logged first difference vs Lag Step
$$ r_{k} = \frac{\sum_{i=1}^{N-k}(Y_{i} - \bar{Y})(Y_{i+k} - \bar{Y})} {\sum_{i=1}^{N}(Y_{i} - \bar{Y})^{2} } $$
- The plot for any step (upto 40) does not plot above 0.2
- There is no signification correlation of logged price with any previous 40 lagged log price
- There is no significant correlation (> 0.2)
- The plot is a random walk
- Seasonality is present if certain lags show high correlation (for Eg: Weekly, Monthly observations)
- Trend is present if certain lags show high correlation (for Eg: Weekly, Monthly observations) and slowly decreases as the lag increases
- Partial Auto Correlation - AdjustedClose Price logged first difference vs Lag Step that is NOT already explained by previous, lower-order lag steps
- Refer auto correlation above
- ARMA (autoregressive moving average) & ARIMA (autoregressive integrated moving average) will be discussed later