Principal Component Analysis (PCA)
Peforms PCA portfolios.
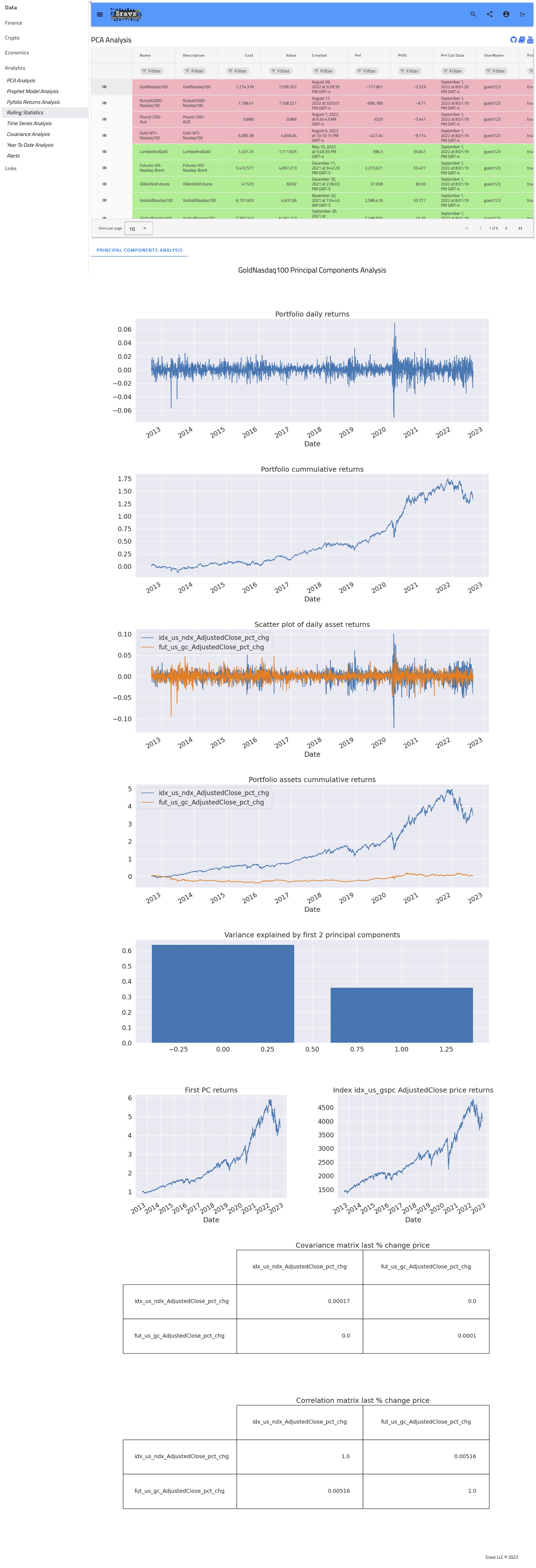
Sravz PCA Analysis - Screenshot
Use Case
- Check the number of Principal components required to describe the variance in a portfolio.
- Suppose there are n assets in a portfolio: There will be
$$ \binom nk=\frac{n!}{k!(n-k)!} $$
assets at a time to perform covariance. - With PCA we select p « n number of predictors to understand the variance in the portfolio.
- If fewer Principal compoments explain most of the variance, the portfolio holdings can be reduced to achive the same diversification (reduce management cost).
PCA Basics
- Dimensionality reduction technique
- PCA is performend on symmetric correlation or covariance matrix
$$ Corr(X,Y)=Corr(Y,X) $$
$$ Cov(X,Y)=Cov(Y,X) $$
- Covariance Matrix is a square matrix giving the covariance between each pair of assets of a given portfolio daily returns vector. Main diagonal contains variances (i.e., the covariance of each asset with itself).
- Correlation Matrix is a square matrix giving the corrleation between each pair of assets of a given portfolio daily returns vector. Main diagonal contains correlation (i.e., the correlation of each asset with itself = 1)
- Both correlation and covariance are positive when the variables move in the same direction and negative when they move in opposite directions.
- The covariance matrix defines the spread (variance) and the orientation (covariance) of the dataset. The direction of the spread of the dataset is computed by eigenvectors and its magnitude by eigenvalues.
- k-dimensional data has k principal components (each asset daily returns in the portfolio gives a principal component).
- Principal Component are linear uncorrelated variables (Orthogonal Matrix)
$$ A^{\top}A = AA^{\top} = I $$
- If T is a linear transformation from a vector space V over a field F into itself and v is a nonzero vector in V, then v is an eigenvector of T if T(v) is a scalar multiple of v. This can be written as:
$$ T(v)=\lambda(v) $$
where λ is a scalar in F, known as the eigenvalue, characteristic value, or characteristic root associated with v. - Perform linear transformation on the covariance matrix
$$ \begin{bmatrix} Var(x) & Cov(x,y)\\ Cov(y,x) & Var(y) \end{bmatrix}\begin{bmatrix} v_1\\ v_2 \end{bmatrix}^T=\begin{bmatrix} \lambda_1\\ \lambda_2 \end{bmatrix}\begin{bmatrix} v_1\\ v_2 \end{bmatrix} $$
where$$ v_1,v_2... $$
are eigenvectors and$$ \lambda_1,\lambda_2... $$
are eigenvalues